Probabilidade Aplicada
Valor Esperado para as caixas de CS2
Introdução
Muitas vezes pode ser confuso entender onde as teorias estatísticas podem ser aplicadas no contexto da Ciência de Dados. Isso é verdade, em especial, para a parte de probabilidade, que aparenta ter seu propósito únicamente para criação de modelos, muitas vezes vista de maneira supérflua por esse motivo - afinal, os algoritmos já existem, então só deveria entender seu propósito e aplicá-los, certo? - Errado, por vários motivos, mas o que darei ênfase nesse artigo é o de que os conceitos básicos de probabilidade podem ser usados para impulsionar uma análise exploratória ou, ainda, gerar um insight final valioso para os stakeholders.
Nesse contexto, será apresentado de maneira prática o uso da Esperança (Valor Esperado), Variância e da Distribuição Binomial.
Estudo de Caso
O uso desses conceitos podem ser aplicados em diversos contextos reais, basta encontrar um contexto em que se encaixe (existem vários!). Nessa análise foi montando um dataset das caixas do jogo CS2. Counter Strike 2 (CS2) é um dos maiores jogos onlines da atualidade, na qual apresenta um sistema de marketplace, onde usuários podem comprar ou vender cosméticos (skins) do jogo. A forma mais comum de conseguir essas skins é através do sistema de caixas, que são como uma roleta de cassino, onde o usuário compra um “ticket” (caixa + chave), que permite ele retirar uma skin aleatória dentro um conjunto de skins pré determinadas que estará presente naquela caixa.

Cada caixa vem com um sub conjunto de skins diferentes e cada skin tem um valor de mercado. Esses valores variam conforme a raridade da skin e por oferta/demanda. A tabela abaixo representa as possíveis raridades das skins:
| Tipo | Prob. de Sair Skin do Tipo: |
|---|---|
| Rare / Mil-Spec (Blue) | 0.7992 |
| Mythical / Restricted (Purple) | 0.1598 |
| Legendary / Classified (Pink) | 0.032 |
| Ancient / Covert (Red) | 0.0064 |
| Exceedingly Rare Special (Gold) | 0.0026 |
Diante disso, o estudo de caso propõe responder à pergunta: dentre as várias caixas presentes no jogo, qual seria a que traz um melhor retorno? Para tal, foi realizado um web scraping dos valores das caixas, bem como os itens contidos nela e seu preço mínimo e máximo. Como o jogo contém várias caixas diferentes, o escopo da coleta de dados se focou apenas naquelas que podem ser conseguidas gratuitamentes, dentre as opções conhecidas como Prime Drop Pool
Análise
Feito o processo de extração e algumas transformações, uma base com a seguinte estrutura foi gerada:
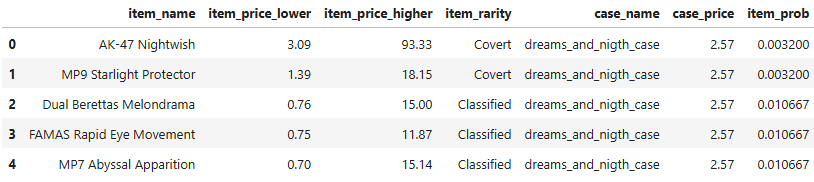
Perceba que a probabilidade dos itens são menores do que as especificadas na Tabela 1. O motivo disso é que cada caixa contém mais de um item com a mesma raridade, fazendo-se necessário a divisão da probabilidade total entre eles. Ou seja, se existem dois itens Covert na caixa dreams_and_nigth, então a probabilidade cada um será a probabilidade total de itens vermelhos divido por 2 (0.0064 / 2).
Outro ponto importante é que foi coletado tanto o maior quanto menor preço daquele item no dia do scraping. Percebe-se que existem altas amplitudes de variação no preço de mesmas skins. Isso ocorre devido a um sistema de “qualidade” de skins que existe no jogo. Esse sistema, conhecido como float, atribui aleatóriamente e não uniformemente um nível de qualidade para a skin ao ser aberta. Como não se tem essas probabilidades, essa parte será desconsiderada da análise.
Inicialmente, a fim de se tentar se aproximar de um valor mais justo, foi considerada a média entre o menor e maior preço.
Com essas ideias em mente, podemos aplicar o conceito de Esperança para encontrar qual seria o valor esperado de retorno sobre uma caixa! A fórmula da Esperança é dado por:

X representa a variável aleatória, o preço, e P a probabilidade dele ocorrer. Você pode pensar, "mas o preço da skin, no contexto do dataset, não é aleatório, como medir o retorno monetário esperado com isso?". O que de fato é aleatório é a qual skin vai cair, porém, apesar do preço ser fixo, ele está atrelado a skin como um atributo seu. É como se o preço a e a skin fossem uma coisa só, ou coisas complementares. Outros atributos poderiam ser: cor, tamanho, quantidade de balas da arma. O ponto é que esse atributo pode ser visto como equivalente a nossa variável aleatória. Dessa forma, nosso X será o preço.
Por sua vez, a Variação é dada por:

Em Python:
df['item_price'] = (df['item_price_lower'] + df['item_price_higher']) / 2
df['expected'] = df['item_price'] * df['item_prob']
df['expected_sq'] = (df['item_price'] ** 2) * df['item_prob']
df_result = df.groupby('case_name').agg(
{
'expected':'sum',
'expected_sq':'sum',
'case_price':'mean',
}
)
df_result['opening_price'] = df_result['case_price'] + 2.5 #key price
df_result['expected_roi'] = (df_result['expected'] - df_result['opening_price']) * 100 / df_result['opening_price']
df_result['var_expected'] = df_result['expected_sq'] - (df_result['expected'] ** 2)
df_result['std_dev'] = df_result['var_expected'] ** 0.5
Com isso, temos o seguinte resultado:
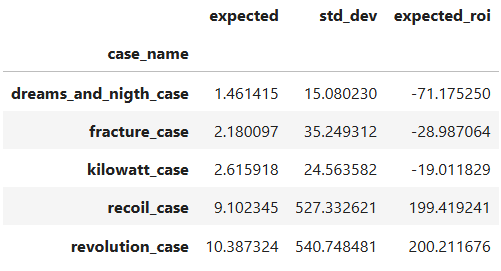
Pelo valor esperado (E), as melhores caixas são a recoil e revolution, tendo o melhor retorno sobre o investimento (ROI). No entanto, devemos nos atentar também ao desvio padrão, que está muito alto, indicando que essas caixas tem um alto grau de variabilidade e risco associado. O valor recebido nas outras caixas podem ser mais certeiros e próximos da realidade, mas como o ROI delas é negativo não parecem ser também uma opção viável. Obviamente, como um sistema de cassino, o esperado dessas caixas é a derrota, então o resultado não é surpreendente. Caso um usuário fosse apostar, provavelmente a melhor escolha fosse a revolution case, já que no acumulado de caixas, ela poderia dar um maior retorno, mesmo com os riscos.
E se formos conservadores? Seguindo o Princípio da Prudência da Contabilidade, onde devemos subestimar os ativos e superestimar os passivos, iremos considerar o menor preço da skin, ao invés da média do maior e menor. Com isso temos um cenário onde nenhuma caixa sequer valeria o risco.
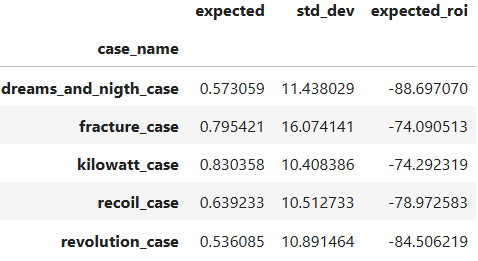
Distribuição Bionomial
Agora suponhamos que eu tenha dinheiro sobrando e queira comprar 100 caixas para conseguir uma skin gold (a mais rara). Quais as chances de eu conseguir pelo menos uma dessas? Podemos responder essa pergunta pela Distribuição Binomial, que tem a seguinte fórmula:

- k é variável que queremos estimar, ou seja, 1 (pelo menos 1 item raro)
- n é o número de tentativas máximo
- p é a probabilidade de sucesso
- (n k) é a combinação de n elementos tomados a k a k
Importante destacar que, para usar essa distruição, os eventos devem ser independentes (são), deve haver um limite superior fixo (100, no exemplo), deve haver somente duas saídas (sair gold skin e não sair gold skin) e probabilidade de sucesso constante (prob. de skin gold é sempre a mesma)
Aplicando a fórmula ao contexto de pelo menos 1: P( k >= 1) = 1 - P(k = 0)
from scipy.stats import binom
n = 100
p = 0.0026
k = 0
prob = 1 - binom.pmf(k, n, p)
Resultado: 22,9% de se obter pelo menos uma skin gold em 100 tentativas.
Conclusões
Percebe-se que não existe um cenário muito promissor nesse sistema do jogo. Idealmente, ele deve ser visto como entreterimento, já que, em média, a pessoa irá perder. Caso ela queira arriscar, a revolution case se mostra a melhor opção. Fazendo pesquisas na internet, parece que o público de fato vê essa caixa como uma das mais promissoras do jogo para tentar a sorte.
Com isso, vemos a utilidade das distribuições probabilistcas de maneira prática, trazendo respostas úteis para aqueles que buscam explicações no mundo da aleatoriedade. Sua utilidade não para por aqui, conforme se conhece mais distribuições e contextos adequados, ampliam-se as possibilidades de aplicação e interpretação dos dados.